数制和编码

真值和机器数

• 真值：符合人类习惯的数字
• 机器数：数字实际存到机器里的形式，正负号需要被数字化

真值	机器数
+15	0 1111
-8	1 1000

BCD码

BCD码：二进制编码的十进制数

二进制数：0、1 方便计算机处理
十进制数：0、1、2、3、4、5、6、7、8、9、10 符合人类习惯

BCD码的计算

进制数	算术式	结果
十进制	5 + 8	13
8421码	0101 + 1000	1101

我们发现1101不在8421码映射表里，8421码中1010~1111没有定义。我们可以在这个运算基础上+6即：1101 + 0110 = 10011即0001 0011也就是13。

进制数	算术式	结果
十进制	9 + 9	18
8421码	1001 + 1001	1 1010

我们发现1 1010不在8421码映射表里，8421码中1010~1111没有定义。我们可以在这个运算基础上+6即：1 1010 + 0110 = 1 1000即0001 1000也就是18。

定点整数，小数

原码表示

对于无符号整数

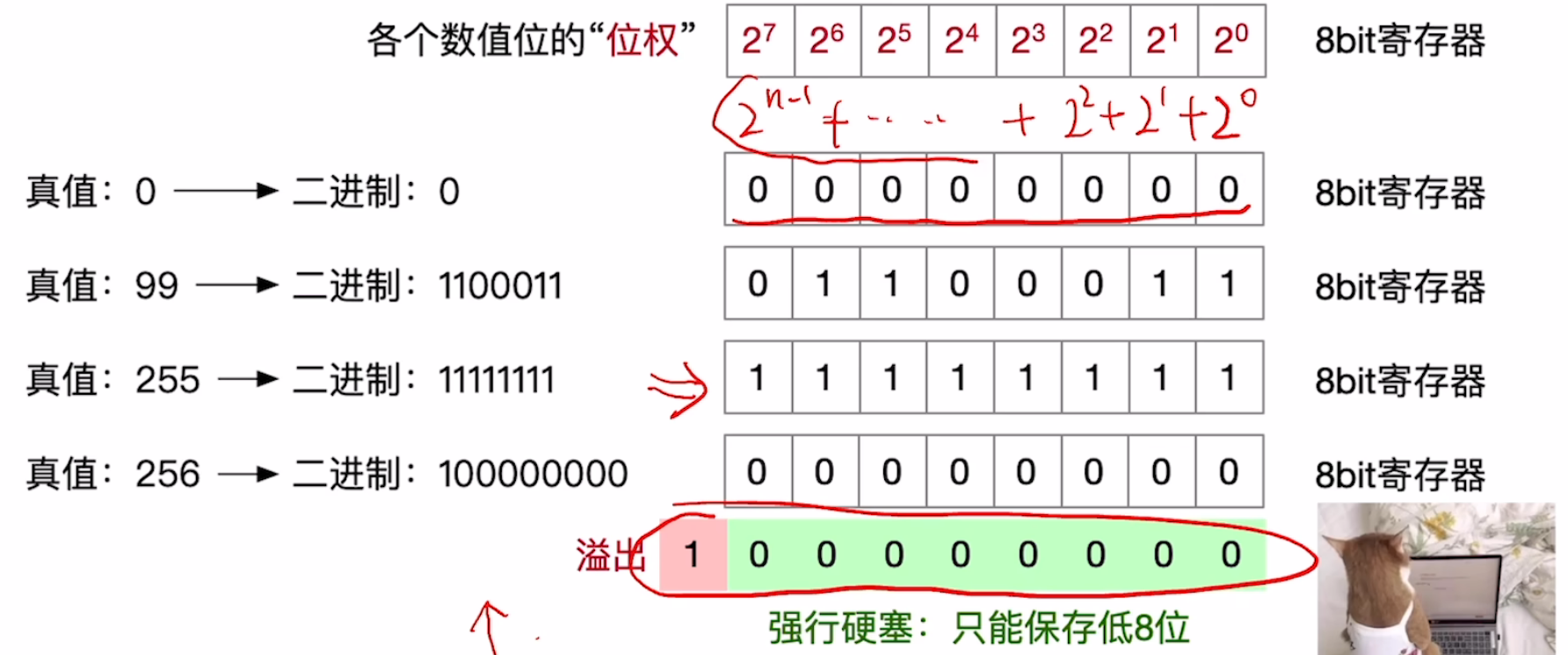
• 全部二进制位都是数值位，没有符号位。
• 若机器字长n + 1位，带符号整数的原码范围：
  $$ 0 \leqslant x \leqslant 2^n - 1 $$

对于有符号整数

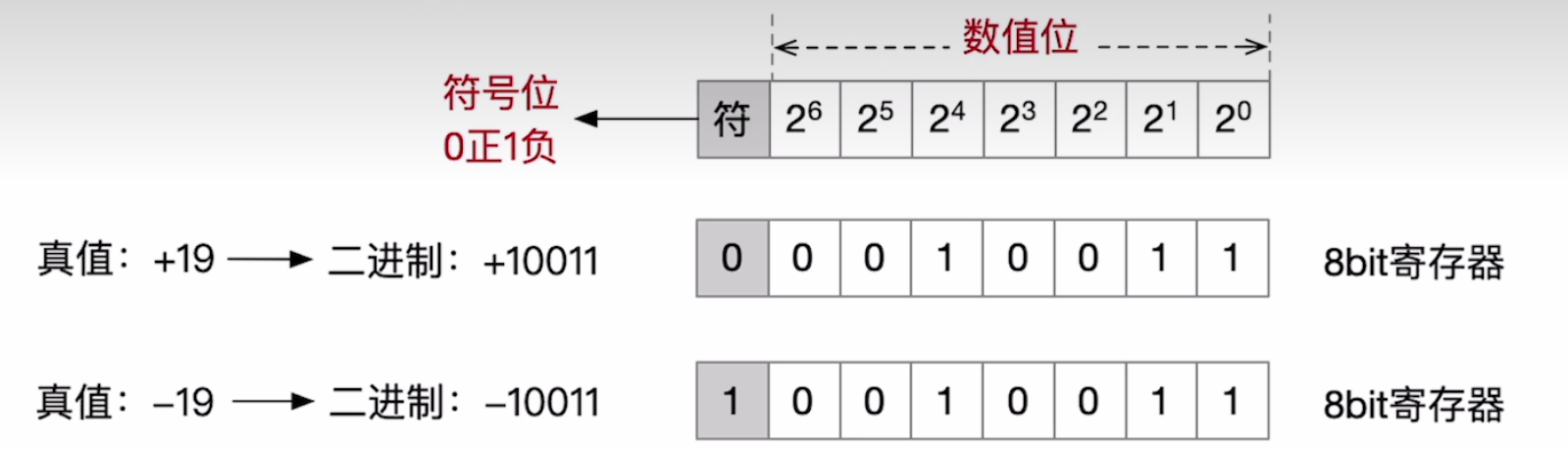
• 最高位是符号位，符号位的0/1对应正/负，剩余的数值为表示真值的绝对值

• 若机器字长为n+1位，原码小数的表示范围：
  $$ -(2^{n} - 1) \leqslant x \leqslant 1 - 2^{-n} $$

• 真值$0$有$+0$和$-0$两种形式

反码表示

• 正数的补码 = 原码。
• 负数的补码 = 原码逐位取反。

	原码	反码
x = +50	[x]原 = 0011 0010	[x]反 = 0011 0010
x = -19	[x]原 = 0001 0011	[x]反 = 1110 1100

若机器字长为n+1位，原码整数的表示范围：

$$ -(2^n - 1) \leqslant x \leqslant 2^n - 1 $$

真值$0$有$+0$和$-0$两种形式

若机器字长为n+1位，原码小数的表示范围：

$$ -(1 - 2^{-n}) \leqslant x \leqslant 1 - 2^{-n} $$

真值$0$有$+0$和$-0$两种形式

补码表示

• 正数的补码 = 原码
• 负数的补码 = 反码末位 + 1（考虑进位）

	原码	反码	补码
x = +50	[x]原 = 0011 0010	[x]反 = 0011 0010	[x]补 = 0011 0010
x = -19	[x]原 = 0001 0011	[x]反 = 1110 1100	[x]补 = 1110 1101

若机器字长为$n+1$位，补码整数的表示范围：

$$ -2^n \leqslant x \leqslant 2^n - 1 $$

移码表示

移码：补码按位取反

	原码	反码	补码	移码
x = +50	[x]原 = 0011 0010	[x]反 = 0011 0010	[x]补 = 0011 0010	[x]移 = 1100 1101
x = -19	[x]原 = 0001 0011	[x]反 = 1110 1100	[x]补 = 1110 1101	[x]补 = 0001 0010

若机器字长为$n+1$位，移码整数的表示范围：

$$ -2^n \leqslant x \leqslant 2^n - 1 $$

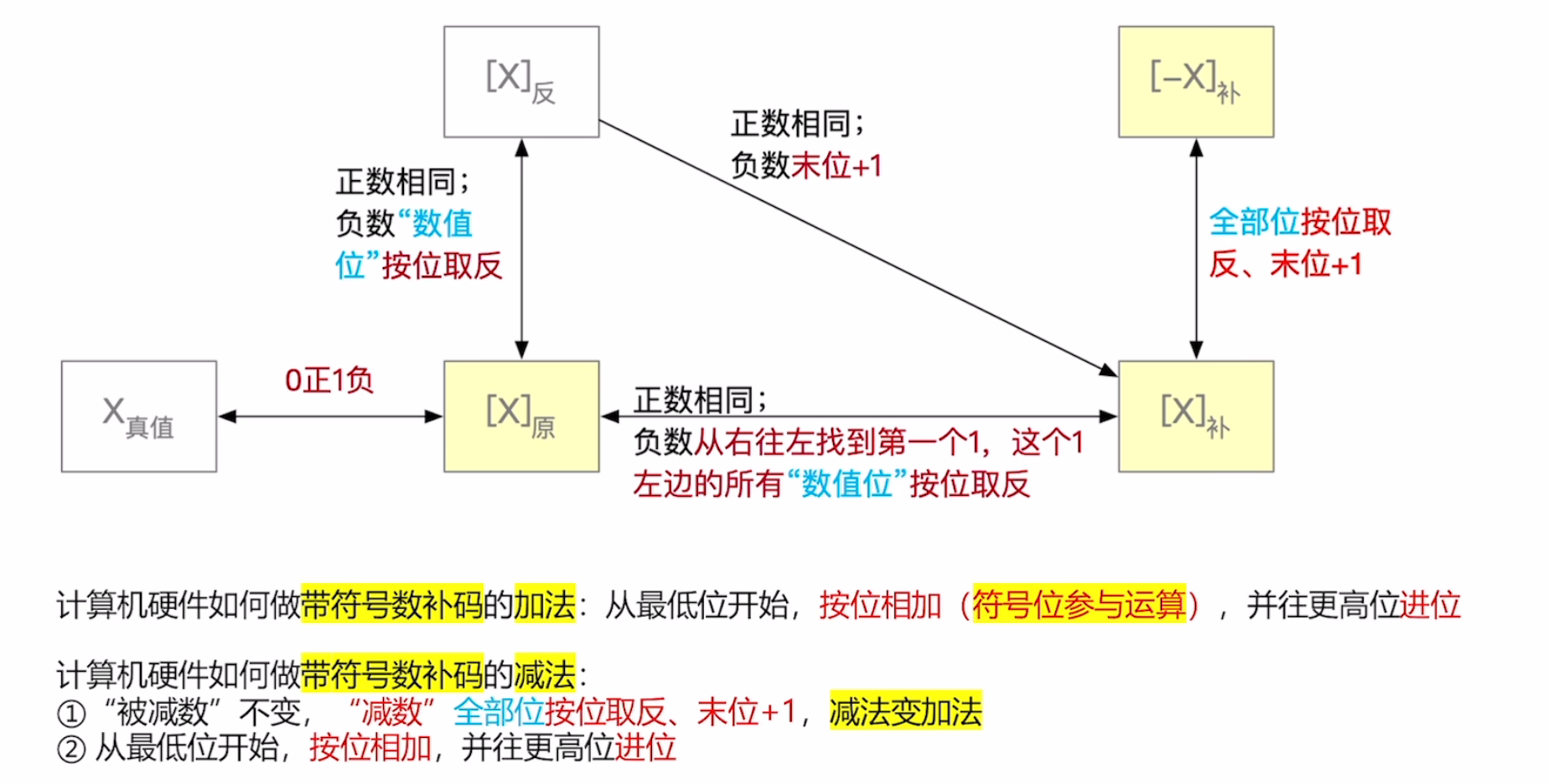
原码，反码，补码的转换

	便于人类理解	中间状态	便于计算机运算
x = +19	[x]原 = 0001 0011	[x]反 = 0001 0011	[x]补 = 0001 0011
x = +50	[x]原 = 0011 0010	[x]反 = 0011 0010	[x]补 = 0011 0010
x = -19	[x]原 = 0001 0011	[x]反 = 1110 1100	[x]补 = 1110 1101
x = -100	[x]原 = 1110 0100	[x]反 = 1001 1011	[x]补 = 1000 1100

无符号整数的运算

加法运算

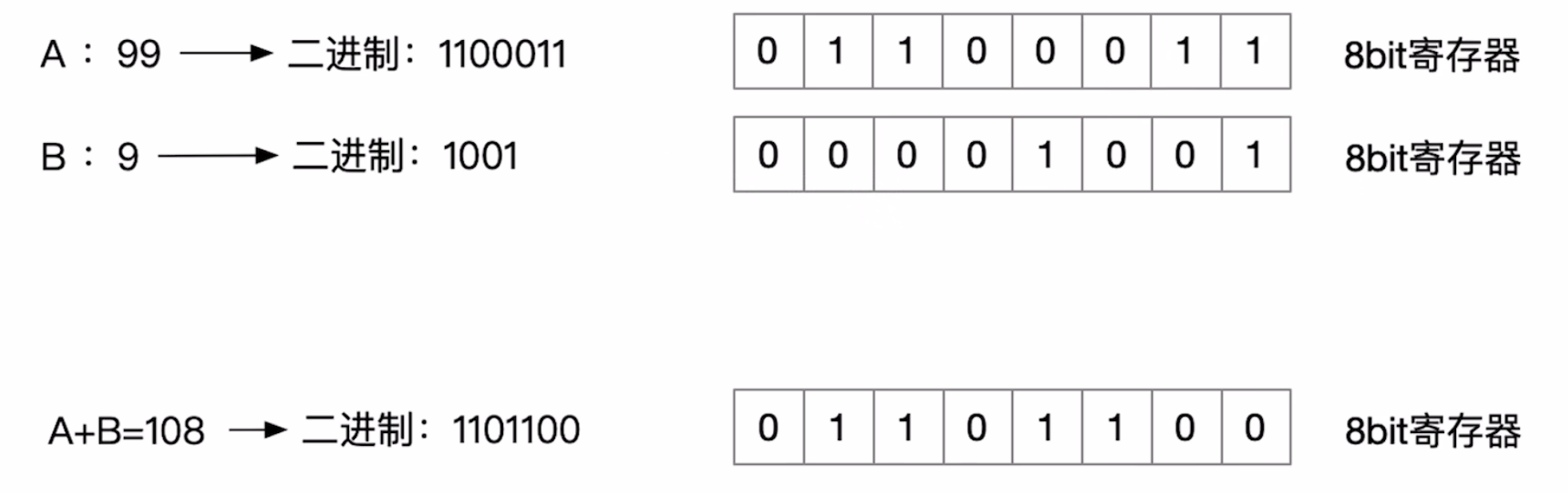
计算机硬件如何做无符号整数的加法：从最低位开始，按位相加，并往刚高位进位

减法运算

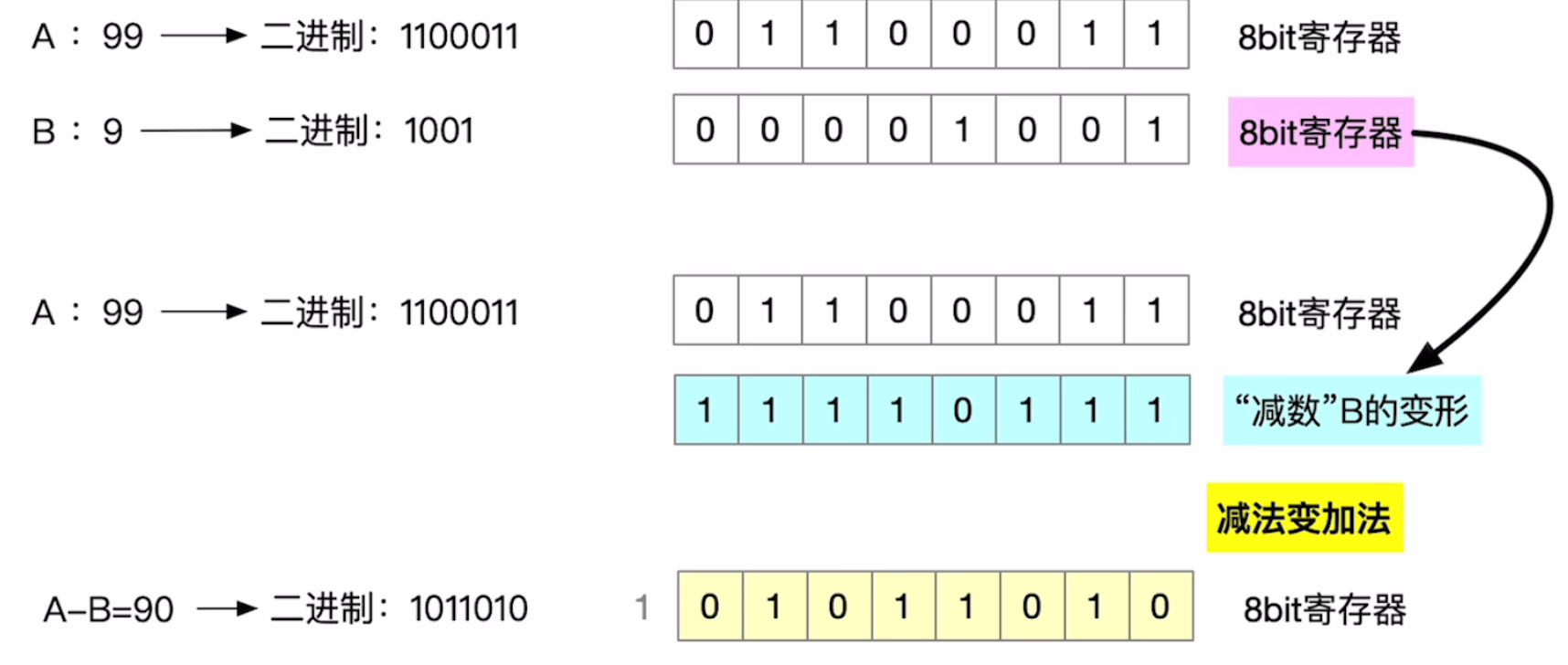
计算机硬件如何做无符号整数的减法：

1. 被减数不变，减数全部位按位取反，末位+1，减法变加法
2. 从最低位开始，按位相加，并往更高位进位

有符号整数的运算

加法运算

• 被减数为负：数字取反，转为补码做加法。
• 被减数为正：转为补码做加法。

A = +19	[x]补 = 0001 0011
B = -19	[x]补 = 1110 1101
A + B = 0	[x]补 = 0000 0000

减法运算

• 被减数为负：转为原码做加法。
• 被减数为正：转为补码做加法。

A = +19	[x]补 = 0001 0011
B = -19	[x]补 = 1110 1101
+B = 19	[x]补 = 0001 0011
A + -B = 38	[x]补 = 0010 0110

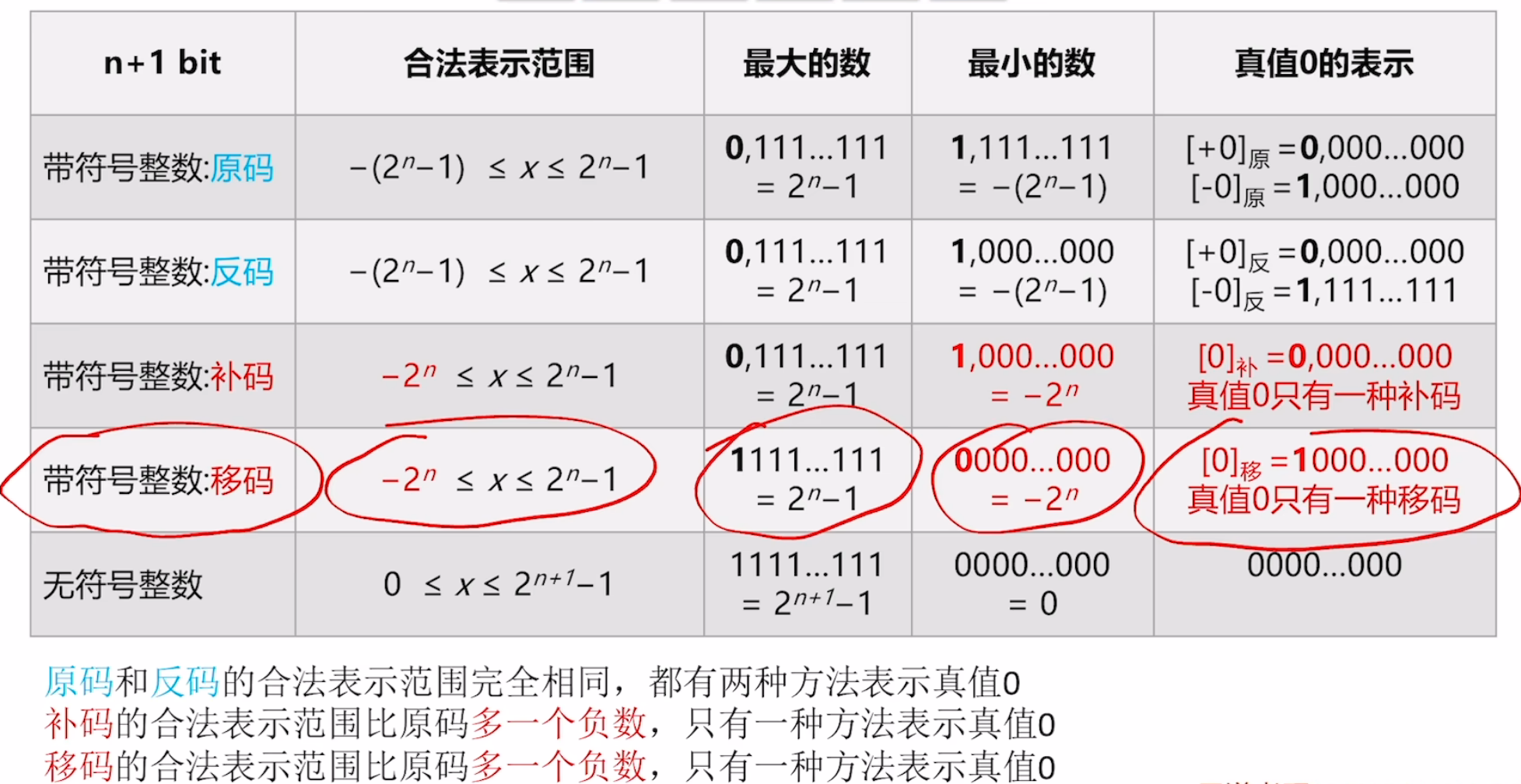
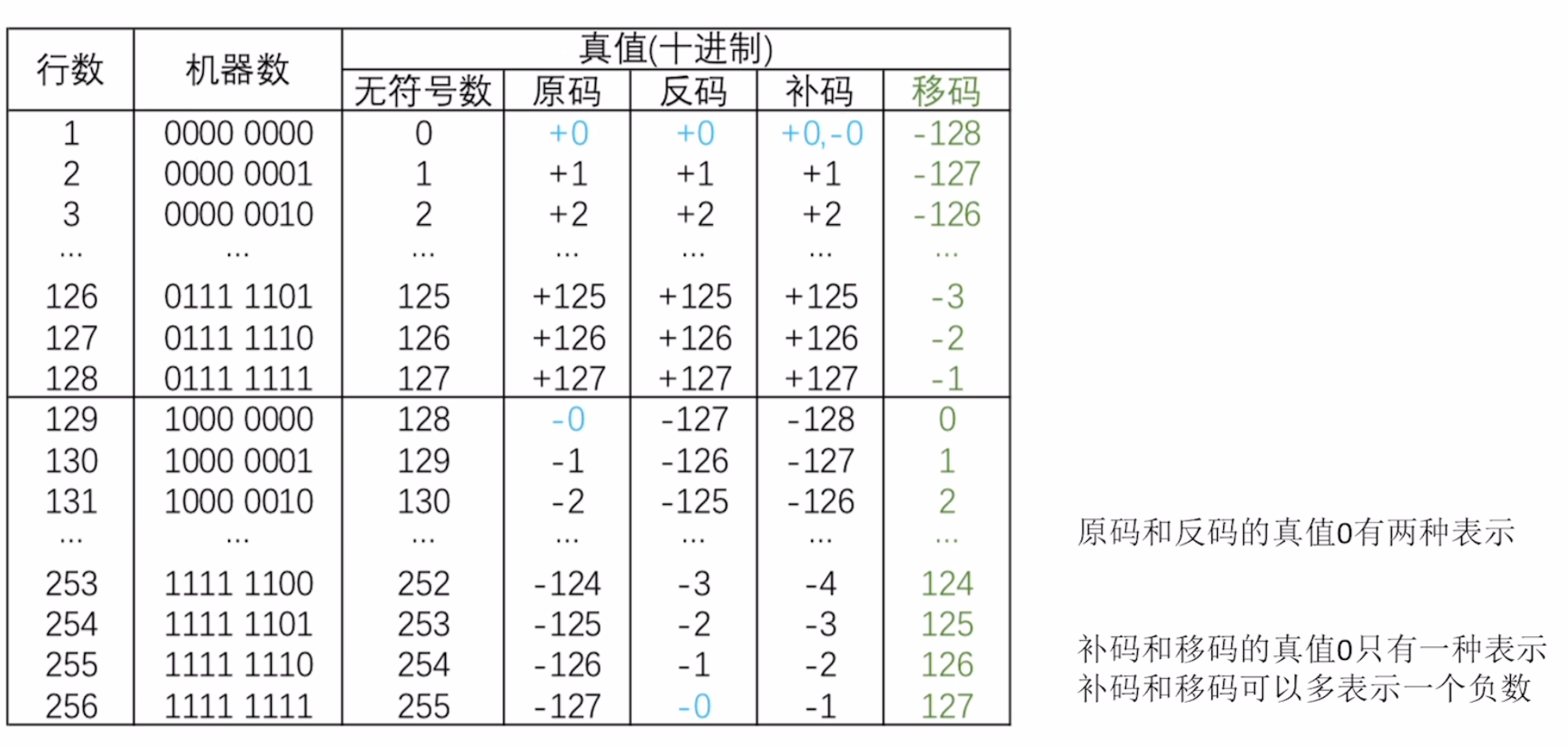
总结

C语言中的强制类型转换

short x = -4321;
unsigned short y = (unsigned short)x;

• short是有符号短整型，占2字节，unsigned short是无符号短整型，占2字节。
• x为有符号数，最高位是符号位。转为无符号数之后，最高位是数值位。类型强制转换后为y = 61215。

int a = 165537, b = -34991;
short c = (short)a, d = (short)b;

short是有符号短整型，占2字节，int是整型，占4字节。整形转为短整形需要截断。

• a = 165537 原码 = 0010 1000 0110 1010 0001。转为short类型后占2字节，原码 = 1000 0110 1010 0001。short是有符号数，最高位1是符号位，所以是-31,071
• b = -34991 补码 = 1111 1111 1111 1111 0111 0111 0101 0001。转为short类型后占2字节，原码 = 1111 0111 0111 0101。short是有符号数，最高位1是符号位，所以是-2,187。